▷차원의 저주
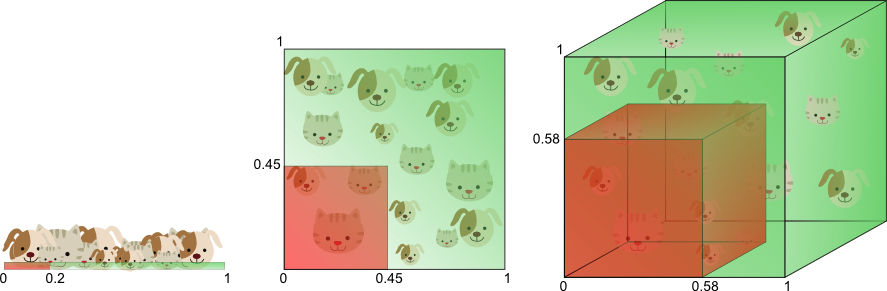
-차원이 증가할수록 변수들의 밀집도가 넓어짐. 따라서 개별 차원 내 학습 데이터의 수가 적어짐.
-예) kNN 모델에서 차원이 커질수록 주변의 데이터들이 멀어짐
-따라서 변수들을 상관관계가 높은 묶음으로 묶고 데이터 차원을 축소해 정제하는 과정이 필요함.
-예) 고전, 프랑스어, 영어 >> 언어 능력
-PCA ( Principal Component Analysis ) : 주성분 분석 - 변수들의 선형 조합에 의해 대표적인 주성분을 만들어 차원을 줄이는 방식(고유분산이 필요 x)
-t-SNE (t-Stochastic Neighbor Embedding) : t-분산 확률적 인접 임베딩 방법을 사용해 데이터를 표시하는 방식 / 확률 분포에 의해 2차원 공간에 mapping 함
-FA (Factor Analysis) : 요인 분석 - 측정변수를 공통적인 요인으로 묶어 자료의 복잡성을 줄이는 방식(고유분산이 중요)
-차원 축소의 장점 : 관측 불가능의 보이지 않는 것들을 측정하기 위해 관측 가능한 요소들을 이용해 연구할 수 있음
-차원 축소의 단점 : 연구 결과가 함축되는 과정에서 연구자의 의도가 개입되고, 데이터의 직관성이 떨어지게 됨
-분산 : 평균값 중심으로 분포된 정도
-공분산 : 두 변수의 관계를 나타내는 양 / 두 변수 간 편차의 곱
▷차원 축소 실습(PCA)
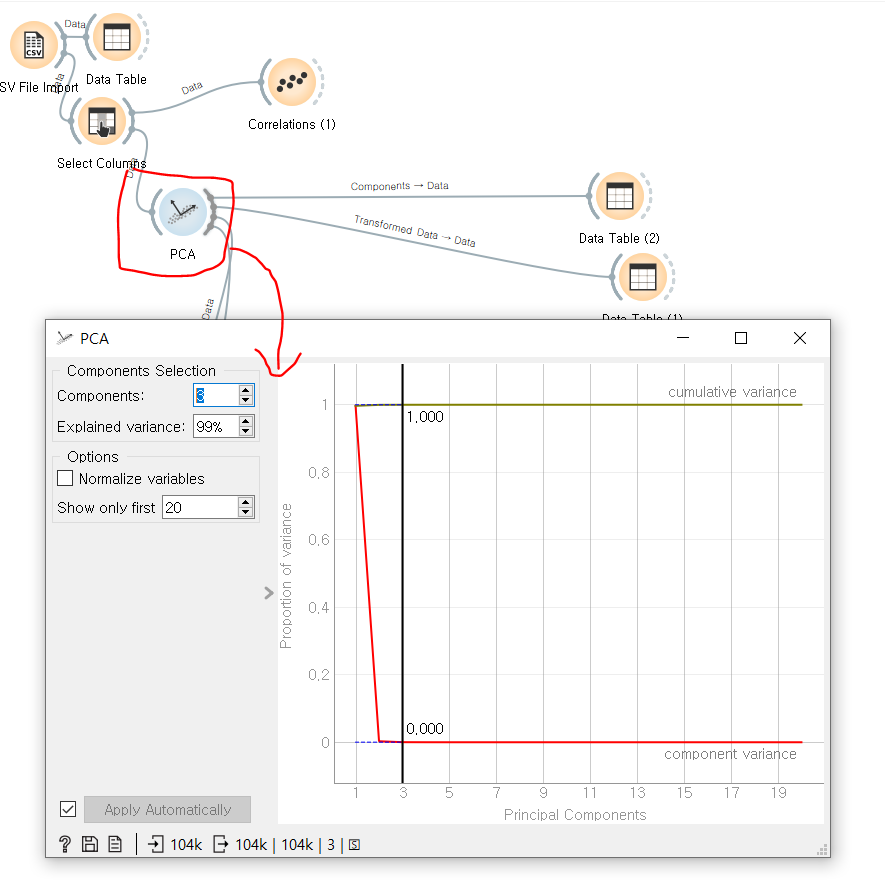
PCA를 사용해 대규모 데이터 세트의 시각화를 단순화활 수 있다. 또 PCA(주성분 분석)을 활용해, 원하는 갯수의 주성분을 구성하고 그 결과를 Data Table 로 확인할 수 있다.
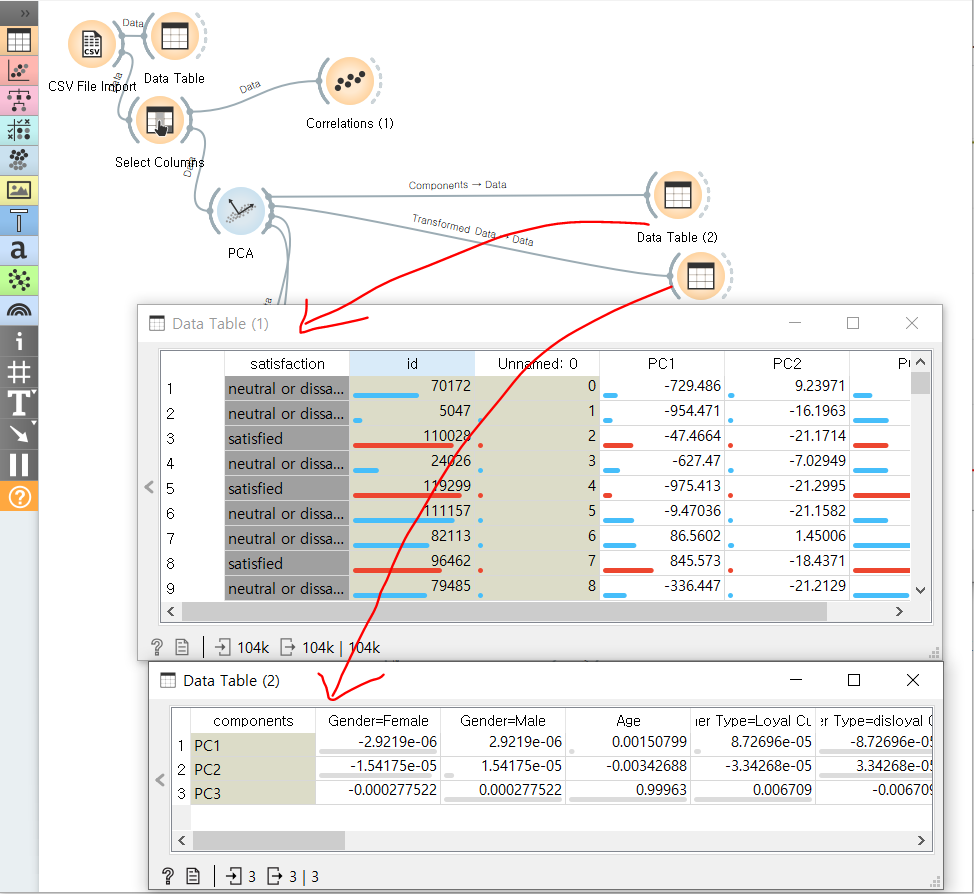
-PCA 는 변환된 데이터와 주 구성 요소 두 가지의 출력을 제공한다. 현재 위에서는 세 가지 주구성요소로 수많은 요소드을 차원축소 시켰다. 위 세가지 주구성 요소의 가중치와 포함 요소들을 확인할 수 있다.
-주성분 분석은 이렇게 대량의 데이터를 단순화 시키지만, 이 과정에서 연구자의 자의적 해석이 심화될 수 있다.
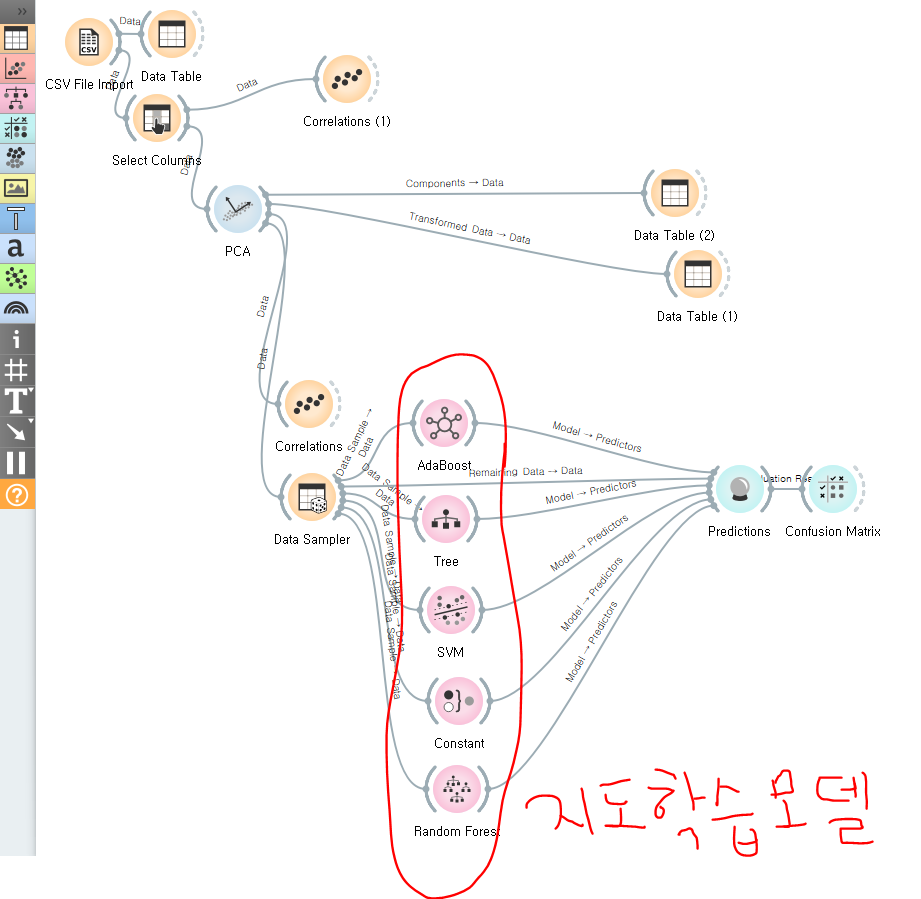
위 예제에서는 PCA 분석 이후 지도학습 모델을 활용해 만족도에 영향을 끼치는 요소들을 분석해 만족/불만족 여부를 예측하는 모델을 구성해보았다.
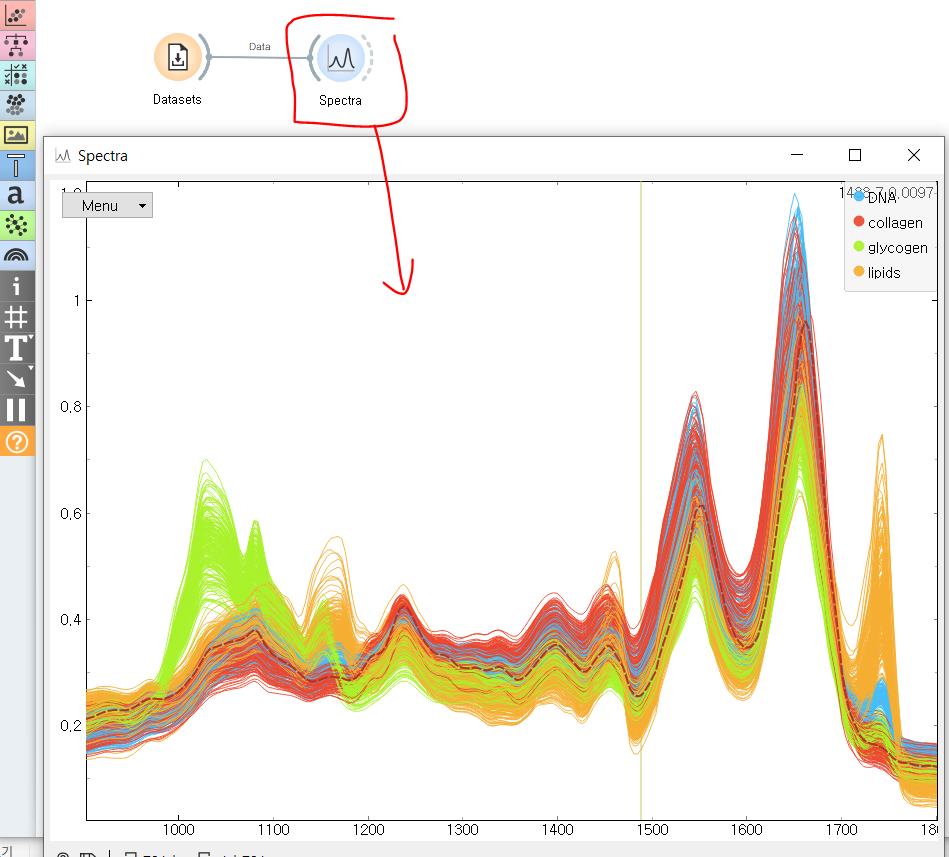
▷분광학 분석(Spectra)
Spectra 위젯을 활용하면 공간정보 없이 일련의 스펙트럼을 시각적으로 탐색할 수 있다.
'교육은 한 사람의 인생을 바꾼다 > AI교육' 카테고리의 다른 글
| 완전 초짜 ORANGE 3 : 내가 분석한 실습예제 (3) | 2021.09.04 |
|---|---|
| 완전 초짜 ORANGE 3 : 비지도학습 군집화 위젯 (0) | 2021.09.03 |
| 완전 초짜 ORANGE 3 : 비지도학습 군집화 기초 (0) | 2021.09.01 |
| 완전 초짜 ORANGE 3 : 지도학습 모델 평가(회귀편) (0) | 2021.08.31 |
| 완전 초짜 ORANGE 3 : 지도학습 모델 평가 (1) | 2021.08.30 |





댓글